給定一組樣本，{1,5},{2,7},{3,9},{4,11},{5,13}，根據樣本預測一元線性方程y=wx+b中的w值和b值，可以用數學的最小二乘法求解，這里使用批量梯度下降法求解。

主要思想：根據y=wx+b計算出來的y值和實際y值是有誤差的，根據這個誤差去更新w和b的值（具體計算公式需要用到偏導數，程序中的變量“xxSum”體現了“批量”），更新速度快慢取決于學習率的大小，當w和b的值幾乎不再更新時，意味計算出來的y值和實際y值的誤差已經很小，這時候停止迭代，求解完成。

#include <iostream>
using namespace std;

void LinearRegression(float x[], float y[], int n, float& w, float& b)
{
	float yOut;
	float residual;
	float deltaB = 0.0;
	float deltaBSum = 0.0;
	float deltaW = 0.0;
	float deltaWSum = 0.0;
	float learningRate = 0.01;

	for (int i = 0; i < n; i++)
	{
		yOut = w * x[i] + b;
		residual = -(yOut - y[i]);
		deltaB = 1 * residual * learningRate;
		deltaBSum = deltaBSum + deltaB;
		deltaW = x[i] * residual * learningRate;
		deltaWSum = deltaWSum + deltaW;
	}

	deltaB = deltaBSum / n;
	deltaW = deltaWSum / n;
	b = b + deltaB;
	w = w + deltaW;
}

int main()
{
	clock_t t1 = clock();

	float x[] = { 1, 2, 3, 4, 5 };	   //樣本x值
	float y[] = { 5, 7, 9, 11, 13 };   //樣本y值
	int n = 5;
	float w = 1.0;	//隨機初始權重
	float b = 1.0;	//隨機初始偏移

	for (int i = 0; i < 1000000; i++)
	{
		float preW = w;
		float preB = b;
		LinearRegression(x, y, n, w, b);
		if (fabs(w - preW) < 0.000001 && fabs(b - preB) < 0.000001)
			break;
	}

	cout << "w=" << w << "," << "b=" << b << endl;
	cout << "線性回歸直線方程：y=" << w << "*x+" << b << endl;

	clock_t t2 = clock();
	cout << "用時" << t2 - t1 << "毫秒" << endl;

	return 0;
}

運行結果如下：

下面驗證以上線性回歸的結果是否正確（其實可以直接觀察到y=2*x+3就是準確解，以上求得的w和b值，與真實值之間的誤差是萬分之幾）。

#include <GL/glut.h>
#include <math.h>

const float ratio = 15.0;
const int pointNum = 5;
const float w = 2.00018;
const float b = 2.99936;

struct Point
{
	float x;
	float y;
};

Point p[pointNum] = { {1,5},{2,7},{3,9},{4,11},{5,13} };

void draw()
{
	glPointSize(1);
	glColor3f(1.0f, 1.0f, 1.0f);

	glBegin(GL_LINES);
	glVertex2f(-1.0, 0);
	glVertex2f(1.0, 0);
	glEnd();

	glBegin(GL_LINES);
	glVertex2f(0, -1);
	glVertex2f(0, 1.0);
	glEnd();

	glPointSize(5);
	glColor3f(1.0f, 0.0f, 0.0f);
	glBegin(GL_POINTS);
	for (int i = 0; i < pointNum; i++)
	{
		glVertex2f(p[i].x / ratio, p[i].y / ratio);
	}
	glEnd();

	glPointSize(3);
	glColor3f(0.0f, 1.0f, 0.0f);

	glBegin(GL_LINES);
	glVertex2f(0.0 / ratio, (w * 0.0 + b) / ratio);
	glVertex2f(10.0 / ratio, (w * 10.0 + b) / ratio);
	glEnd();

	glFlush();
}

void myDisplay()
{
	glClear(GL_COLOR_BUFFER_BIT);
	draw();
}

int main(int argc, char* argv[])
{
	glutInit(&argc, argv);
	glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH);
	glutInitWindowPosition(100, 100);
	glutInitWindowSize(600, 600);
	glutCreateWindow("Draw");
	glutDisplayFunc(myDisplay);
	glutMainLoop();
	return 0;
}

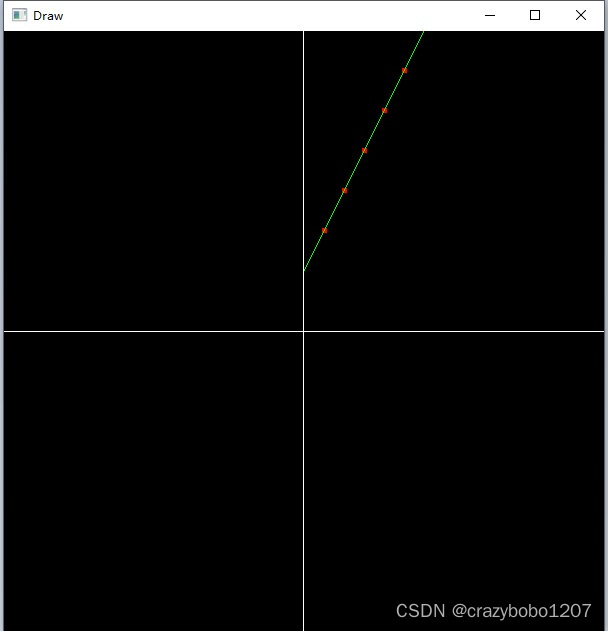
畫出5個樣本點，以及y=2.00018*x+2.99936的直線方程，直線基本穿過5個樣本點。