網站首頁 編程語言 正文
B+樹
B+樹是B樹的一種變體,也屬于平衡多路查找樹,大體結構與B樹相同,包含根節點、內部節點和葉子節點。多用于數據庫和操作系統的文件系統中,由于B+樹內部節點不保存數據,所以能在內存中存放更多索引,增加緩存命中率。另外因為葉子節點相連遍歷操作很方便,而且數據也具有順序性,便于區間查找。
B+樹特點
- B+樹可以定義一個m值作為預定范圍,即m路(階)B+樹。
- 根節點可能是葉子節點,也可能是包含兩個或兩個以上子節點的節點。
- 內部節點如果擁有k個關鍵字則有k+1個子節點。
- 非葉子節點不保存數據,只保存關鍵字用作索引,所有數據都保存在葉子節點中。
- 非葉子節點有若干子樹指針,如果非葉子節點關鍵字為k1,k2,…kn,其中n=m-1,那么第一個子樹關鍵字判斷條件為小于k1,第二個為大于等于k1而小于k2,以此類推,最后一個為大于等于kn,總共可以劃分出m個區間,即可以有m個分支。(判斷條件其實沒有嚴格的要求,只要能實現對B+樹的數據進行定位劃分即可,有些實現使用了m個關鍵字來劃分區間,也是可以的)
- 所有葉子節點通過指針鏈相連,且葉子節點本身按關鍵字的大小從小到大順序排列。
- 自然插入而不進行刪除操作時,葉子節點項的個數范圍為[floor(m/2),m-1],內部節點項的個數范圍為[ceil(m/2)-1,m-1]。
- 另外通常B+樹有兩個頭指針,一個指向根節點一個指向關鍵字最小的葉子節點。
- 在進行刪除操作時,涉及到索引節點填充因子和葉子節點填充因子,一般可設葉子節點和索引節點的填充因子都不少于50%。
以下是一棵4階B+樹,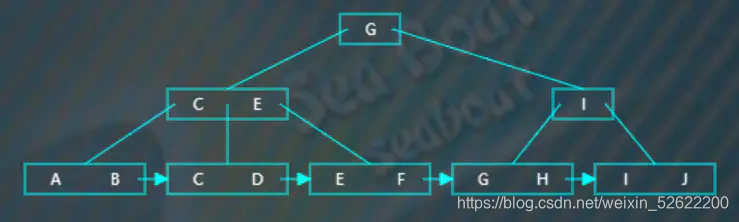
插入操作
假設現在構建一棵四階B+樹,開始插入“A”,直接作為根節點,
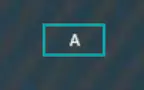
插入“B”,大于“A”,放右邊,
插入“C”,按順序排到最后,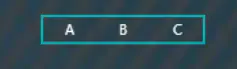
繼續插入“D”,直接添加的結果如下圖,此時超過了節點可以存放容量,對于四階B+樹每個節點最多存放3個項,此時需要執行分裂操作,
分裂操作為,先選取待分裂節點中間位置的項,這里選“C”,然后將“C”項放到父節點中,因為這里還沒有父節點,那么直接創建一個新的父節點存放“C”,而原來小于“C”的那些項作為左子樹,原來大于等于“C”的那些項作為右子樹。這里注意下非葉子節點存放的都是關鍵字,用作索引的,所以父節點存放的“C”項不包括數據,數據仍然存放在右子樹。此外,還需要添加一個指針,由左子樹指向右子樹。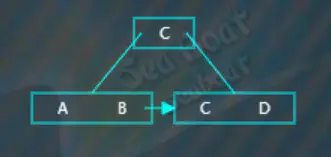
繼續插入“M”,“M”大于“C”,往右子節點,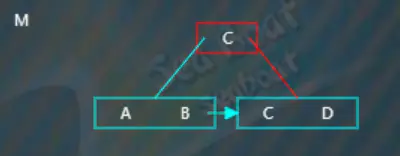
分別與“C”“D”比較,大于它們,放到最右邊,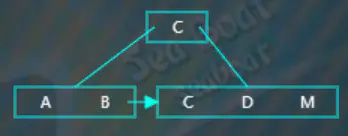
插入“L”,“L”大于“B”,往右子樹,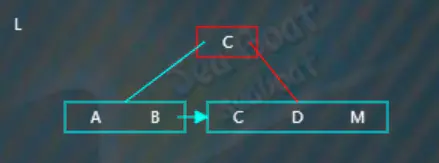
“L”逐一與節點內項的值比較,根據大小放到指定位置,此時觸發分裂操作,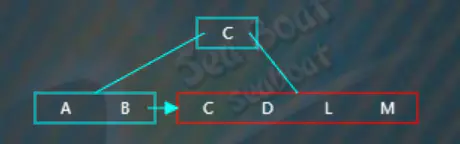
選取待分裂節點中間位置的項“L”,然后將“L”項放到父節點中,按大小順序將“L”放到指定位置,而原來小于“L”的那些項作為左子樹,原來大于等于“L”的那些項作為右子樹。父節點存放的“L”項不包括數據,數據仍然存放在右子樹。此外,還需要在左子樹中添加一個指向右子樹的指針。
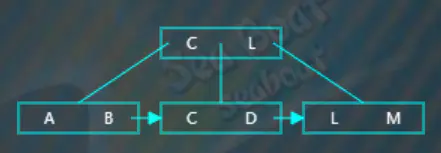
繼續插入“K”,從根節點開始查找,逐一比較關鍵字,“K”大于“C”而小于“L”,往第二個分支,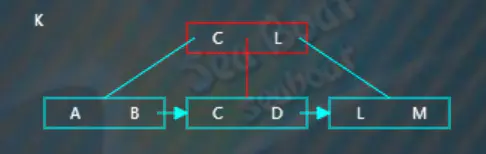
在子節點中逐一比較,“K”最終落在最右邊,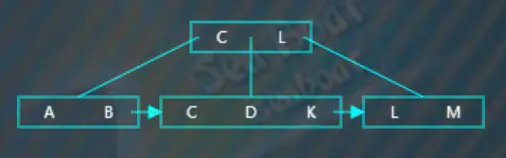
繼續插入“J”,從根節點開始查找,逐一比較關鍵字,“J”大于“C”而小于“L”,往第二個分支,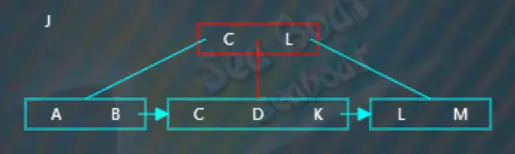
在子節點中找到“J”的相應位置,此時超過了節點的容量,需要進行分裂操作,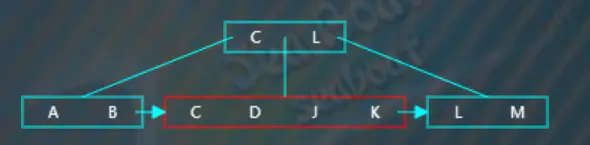
選取待分裂節點中間位置的項“J”,然后將“J”項放到父節點中,按大小順序將“J”放到指定位置,而原來小于“J”的那些項作為左子樹,原來大于等于“J”的那些項作為右子樹。父節點存放的“J”項不包括數據,數據仍然存放在右子樹。此外,還需要在左子樹中添加一個指向右子樹的指針。
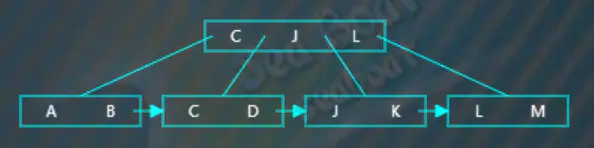
繼續插入“I”,從根節點開始查找,逐一比較關鍵字,“I”大于“C”而小于“J”“L”,往第二個分支,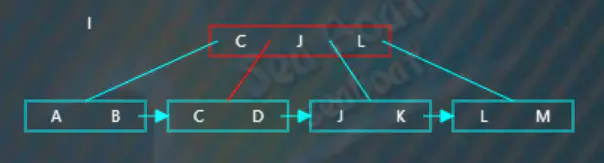
逐一比較找到“I”的插入位置,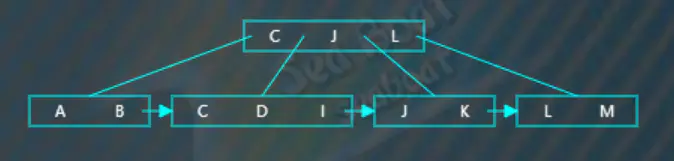
繼續插入“H”,從根節點開始查找,逐一比較關鍵字,“H”大于“C”而小于“J”“L”,往第二個分支,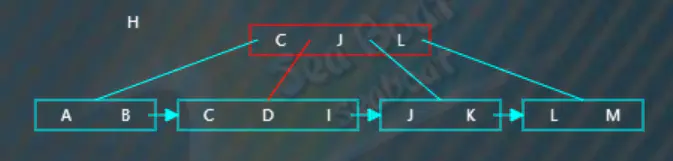
“H”逐一與節點內的值比較,根據大小放到指定位置,此時觸發分裂操作,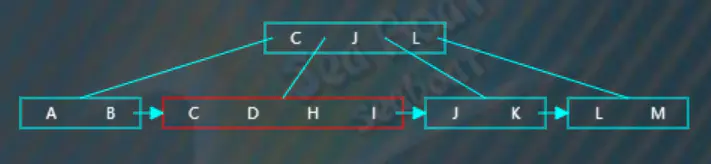
選取待分裂節點中間位置的項“H”,然后將“H”項放到父節點中,按大小順序將“H”放到指定位置,而原來小于“H”的那些項作為左子樹,原來大于等于“H”的那些項作為右子樹。父節點存放的“H”項不包括數據,數據仍然存放在右子樹。此外,還需要在左子樹中添加一個指向右子樹的指針。
但此時父節點超出了容量,父節點需要繼續分裂操作,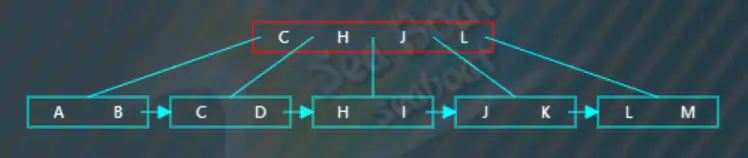
選取待分裂節點中間位置的項“J”,然后將“J”項放到父節點中,但還不存在父節點,需要創建一個作為父節點。原來小于“J”的那些項作為左子樹,原來大于“J”的那些項作為右子樹。這是非葉子節點的分裂,操作對象都是用作索引的關鍵字,不必考慮數據存放問題。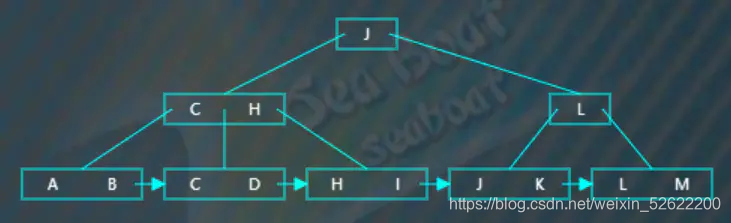
插入“G”,從根節點開始查找,“G”小于“J”,往第一個分支,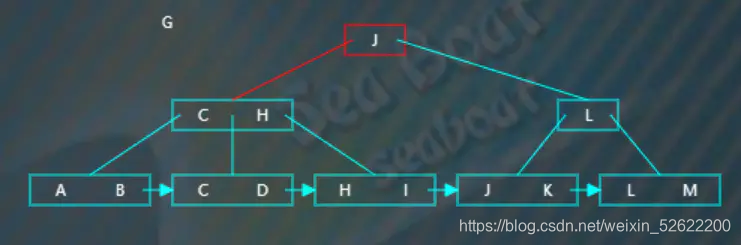
逐一比較節點內項的值,“G”大于“C”小于“H”,往第二個分支,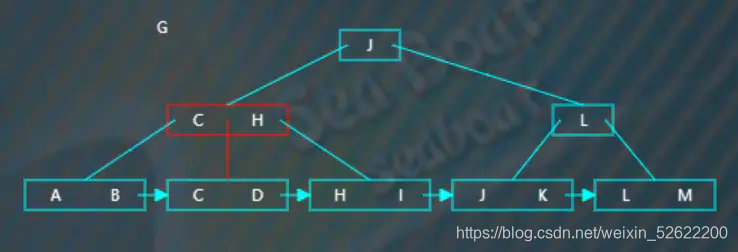
逐一比較節點內項的值,找到“G”的位置并插入,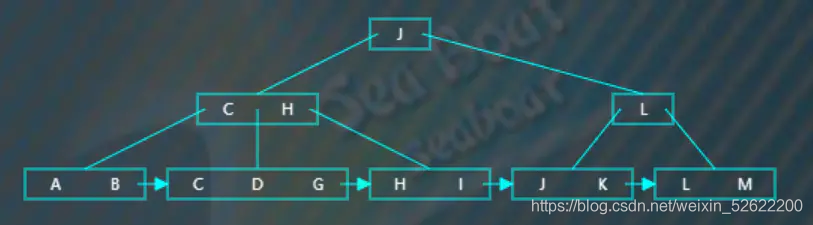
插入“F”,從根節點開始查找,“F”小于“J”,往第一個分支,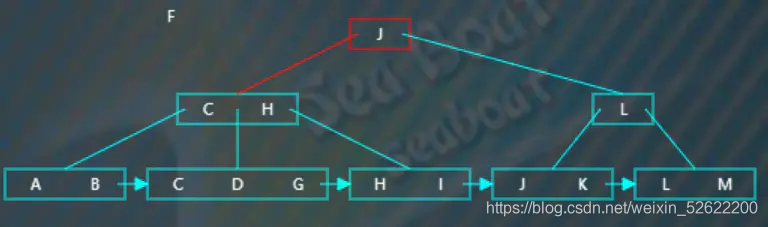
逐一比較節點內項的值,“F”大于“C”小于“H”,往第二個分支,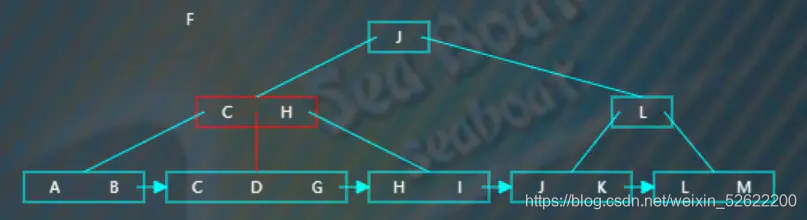
逐一比較節點內項的值,找到“F”的位置并插入,此時觸發分裂操作,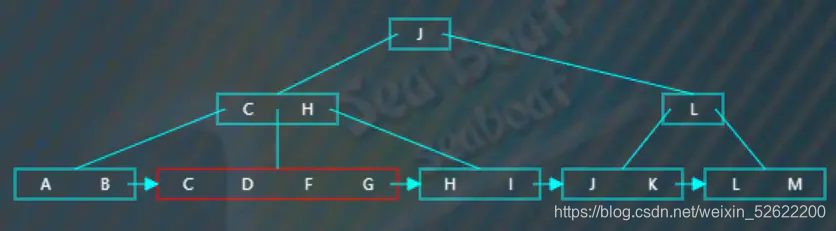
選取待分裂節點中間位置的項“F”,然后將“F”項放到父節點中,按大小順序將“F”放到指定位置,而原來小于“F”的那些項作為左子樹,原來大于等于“F”的那些項作為右子樹。父節點存放的“F”項不包括數據,數據仍然存放在右子樹。此外,還需要在左子樹中添加一個指向右子樹的指針。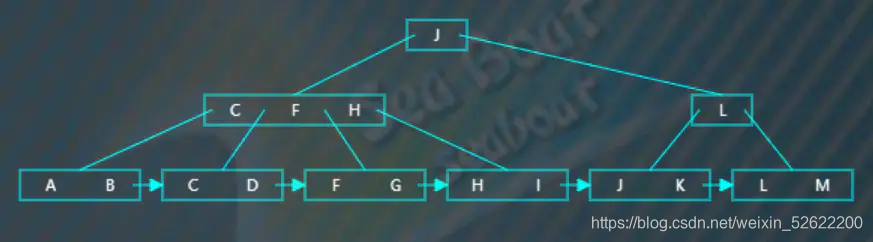
最后插入“E”,從根節點開始查找,“E”小于“J”,往第一個分支,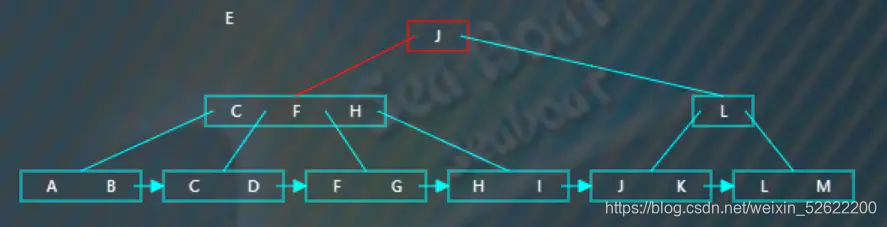
逐一比較節點內項的值,“E”大于“C”小于“F”,往第二個分支,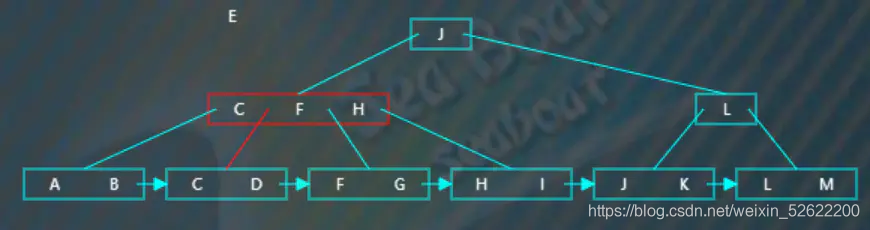
逐一比較節點內項的值,找打“E”適當的位置并插入。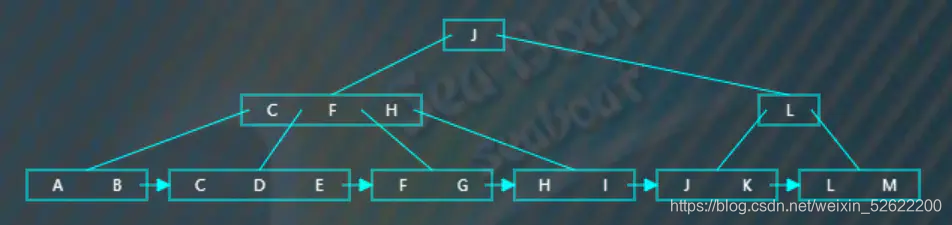
從上面插入操作可以總結,插入主要就是涉及到分裂操作,而且要注意到非節點只保存了關鍵字作為索引,而數據都保存在葉子節點上,此外還需要使用指針將葉子節點連接起來。最終我們可以看到葉子節點的項按從小到大排列,因為有了指針使得可以很方便遍歷數據。
查找操作
對B+樹的查找與B樹的查找差不多,從根節點開始查找,通過比較項的值找到對應的分支,然后繼續往子樹上查找。
比如查找“H”,“H”小于“J”,往第一個分支,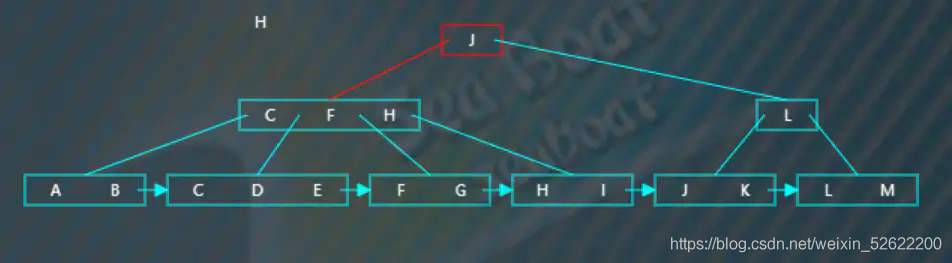
逐一比較節點中的項,發現應該往第四個分支,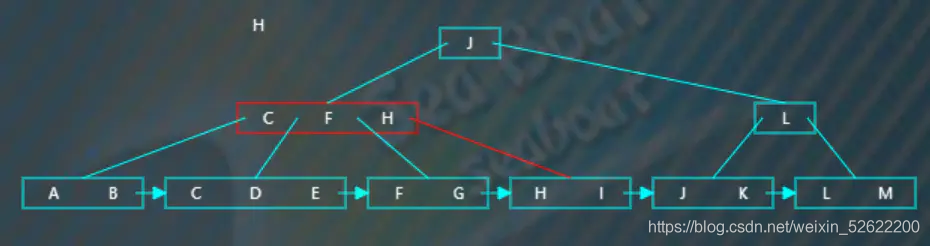
逐一比較,找到“H”。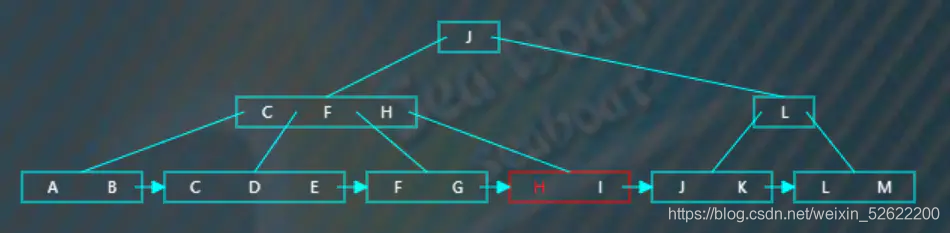
遍歷操作
遍歷操作首先是要先找到樹最左邊的葉子節點,然后就可以通過指針完成整棵樹的遍歷了。
從根節點開始,一直往第一個分支走,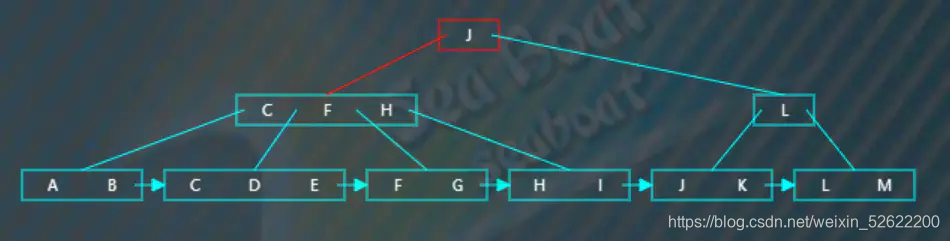
繼續往第一個分支走,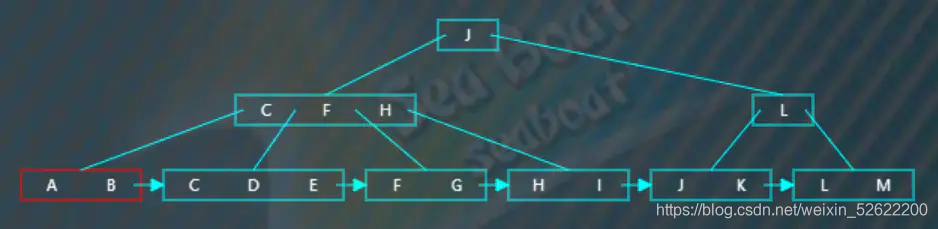
第一個葉子節點有兩個項,接著根據指針跳到第二個葉子節點,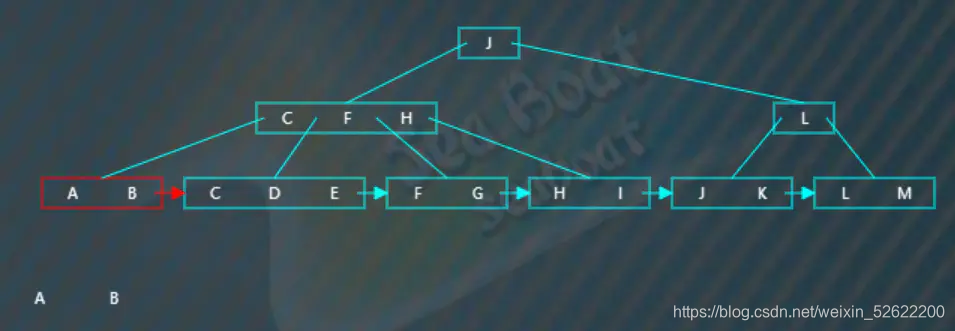
第二個節點有三個項,根據指針繼續往下一個節點,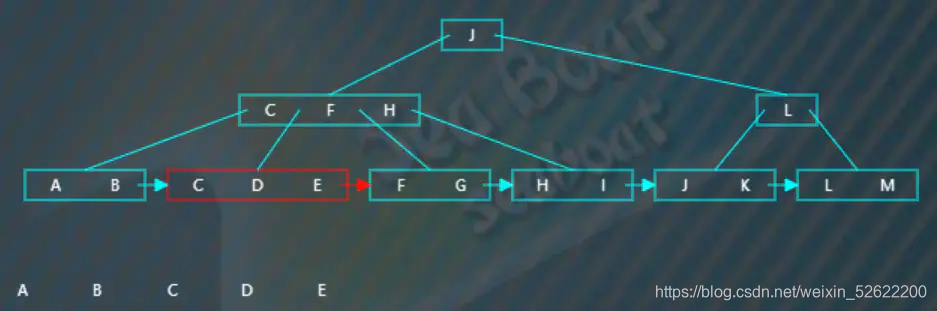
該節點有兩個項,根據指針繼續往下一個節點,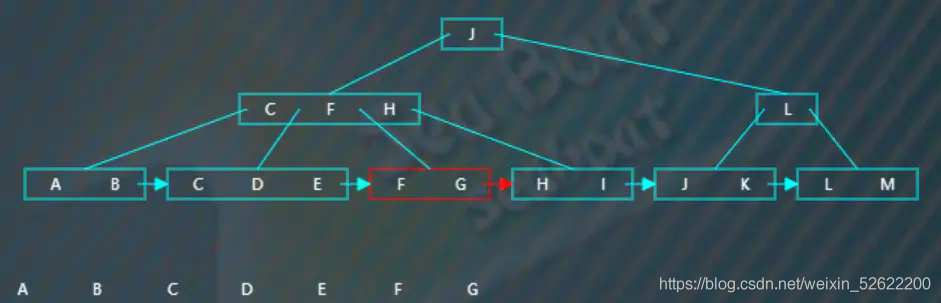
不斷根據指針往下,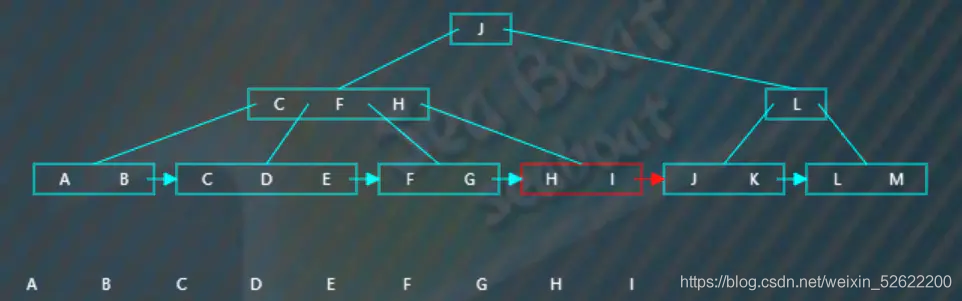
往下,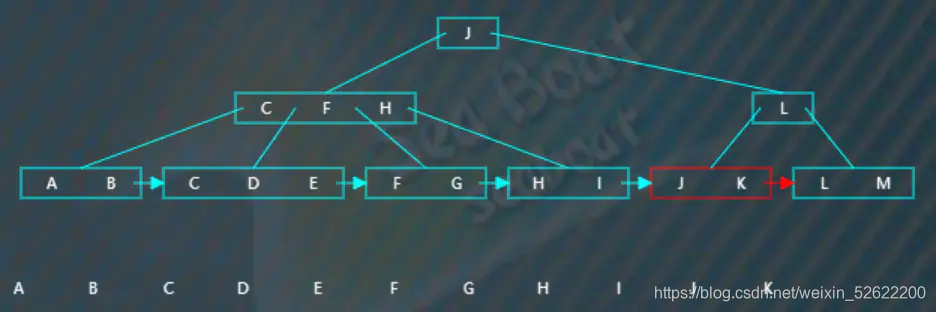
完成整棵樹的遍歷。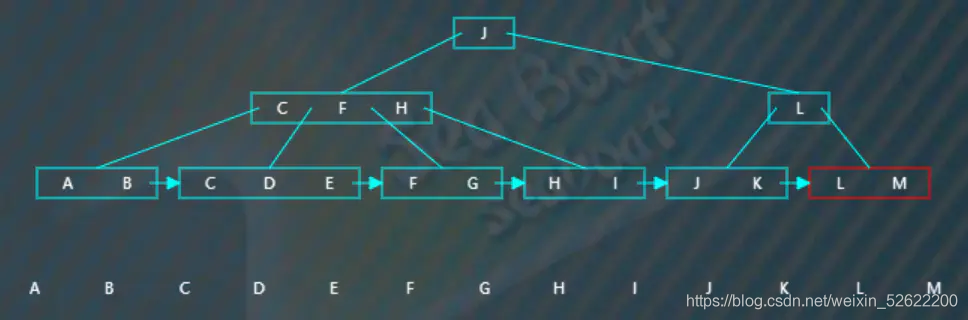
?
原文鏈接:https://blog.csdn.net/qq_43985303/article/details/132340168
- 上一篇:沒有了
- 下一篇:沒有了
相關推薦
- 2022-06-16 golang組件swagger生成接口文檔實踐示例_Golang
- 2022-11-05 docker中nginx卸載、安裝、配置及掛載詳細教程_docker
- 2023-04-29 Linux?grep?-q用法示例詳解_linux shell
- 2022-12-24 Python創建增量目錄的代碼實例_python
- 2022-07-03 golang defer,func()閉包,panic ,recover,contex
- 2022-04-30 Qt數據庫應用之實現通用數據庫分頁_C 語言
- 2023-10-25 用原生promise特性替代async/await解決異步的方法
- 2022-07-17 一起詳細聊聊C#中的Visitor模式_C#教程
- 欄目分類
-
- 最近更新
-
- window11 系統安裝 yarn
- 超詳細win安裝深度學習環境2025年最新版(
- Linux 中運行的top命令 怎么退出?
- MySQL 中decimal 的用法? 存儲小
- get 、set 、toString 方法的使
- @Resource和 @Autowired注解
- Java基礎操作-- 運算符,流程控制 Flo
- 1. Int 和Integer 的區別,Jav
- spring @retryable不生效的一種
- Spring Security之認證信息的處理
- Spring Security之認證過濾器
- Spring Security概述快速入門
- Spring Security之配置體系
- 【SpringBoot】SpringCache
- Spring Security之基于方法配置權
- redisson分布式鎖中waittime的設
- maven:解決release錯誤:Artif
- restTemplate使用總結
- Spring Security之安全異常處理
- MybatisPlus優雅實現加密?
- Spring ioc容器與Bean的生命周期。
- 【探索SpringCloud】服務發現-Nac
- Spring Security之基于HttpR
- Redis 底層數據結構-簡單動態字符串(SD
- arthas操作spring被代理目標對象命令
- Spring中的單例模式應用詳解
- 聊聊消息隊列,發送消息的4種方式
- bootspring第三方資源配置管理
- GIT同步修改后的遠程分支
